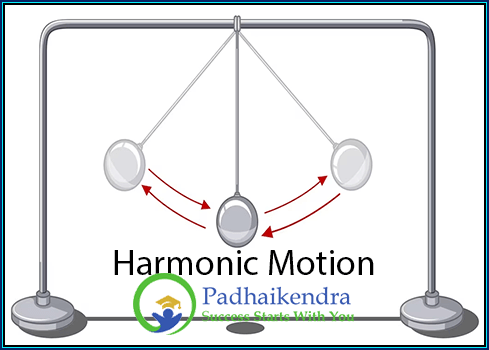
The simple pendulum oscillates due to the interplay between two opposing forces: the force of gravity and the tension force in the pendulum’s string or wire. When the pendulum is displaced from its equilibrium position, gravity pulls the mass downward, causing it to accelerate toward the equilibrium position. As the mass moves back toward the equilibrium position, the tension force in the string or wire pulls it back, causing it to decelerate. This process repeats as the pendulum swings back and forth, causing it to oscillate.
The length of the pendulum is an important factor in determining the frequency and time period of its oscillations. The time period of a simple pendulum is the time it takes for one complete oscillation. It is directly proportional to the square root of the length of the pendulum and inversely proportional to the square root of the acceleration due to gravity.
The oscillations of a simple pendulum can be affected by various factors such as air resistance, friction at the point of suspension, and non-uniformities in the pendulum’s mass distribution. These factors can cause the pendulum’s motion to deviate from the idealized simple harmonic motion, but can also be minimized by careful design and construction of the pendulum.
The motion of a simple pendulum is governed by fundamental principles of physics and is a useful model for understanding a wide range of natural phenomena, from the motion of celestial bodies to the behavior of atoms and molecules.
What keeps the simple pendulum oscillating in a simple Harmonic Motion FAQs
Several factors contribute to the oscillations of a system. These include the presence of a restoring force, the system's initial displacement or disturbance from equilibrium, the system's mass or inertia, and the absence of significant damping or external forces. These factors collectively determine the characteristics of the oscillatory motion.
The underlying factor that sustains the oscillations of a simple pendulum is the interplay between gravity and the tension in the pendulum string or rod. These forces work together to keep the pendulum bob swinging back and forth.
When the simple pendulum is displaced from its equilibrium position, gravity acts as a restoring force. It pulls the pendulum bob back towards the equilibrium position, opposing the displacement. This force causes the pendulum to oscillate back and forth.
Gravity is the force responsible for maintaining the simple pendulum in a state of simple harmonic motion. It acts as the restoring force that pulls the pendulum bob back towards its equilibrium position when it is displaced.
The driving force behind the oscillatory motion of a pendulum is the force of gravity. When the pendulum bob is displaced from its equilibrium position, gravity acts as the restoring force that brings it back towards the center.
The fundamental reason for a system to exhibit oscillations in simple harmonic motion is the presence of a restoring force that is directly proportional to the displacement from the equilibrium position. This restoring force provides the necessary conditions for periodic back-and-forth motion.
The primary cause of oscillation in an oscillator is the presence of a restoring force. This force ensures that when the oscillator is displaced from its equilibrium position, it experiences a force that brings it back towards the equilibrium, resulting in oscillatory motion.
The period of a simple pendulum can be calculated using the equation: T = 2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. This equation demonstrates the relationship between the length and period of a simple pendulum.
The oscillations of a simple pendulum can be affected by various factors such as air resistance, friction at the point of suspension, and non-uniformities in the pendulum’s mass distribution. These factors can cause the pendulum’s motion to deviate from the idealized simple harmonic motion, but can also be minimized by careful design and construction of the pendulum.
